1. Atomic Number Of An Atom Is The
2. Atomic Number Of An Atom Represents
3. Atomic Number Of An Atom Or Element Is The Number Of
4. What Does The Atomic Number Tell Us
5. What Does Atomic Number Mean
6. Atomic Number Of An Atom

Overview of Atomic Structure

Atoms are made up of particles called protons, neutrons, and electrons, which are responsible for the mass and charge of atoms.

Learning Objectives

Chemistry, 22:10 nurikchan. What is the atomic number of the atom. Atomic Number - A number representing the positive charge or number of protons in the nucleus of an atom. Of an element never changes, meaning that the number of protons in the nucleus Nucleus - The center of an atom containing protons and neutrons. The atomic number is the number of protons an atom has. It is characteristic and unique for each element. The atomic mass (also referred to as the atomic weight) is the number of protons and neutrons in an atom. Atoms of an element that have differing numbers of neutrons (but a constant atomic number) are termed isotopes. Isotopes, shown in.

Discuss the electronic and structural properties of an atom

Key Takeaways

Key Points

• An atom is composed of two regions: the nucleus, which is in the center of the atom and contains protons and neutrons, and the outer region of the atom, which holds its electrons in orbit around the nucleus.
• Protons and neutrons have approximately the same mass, about 1.67 × 10-24 grams, which scientists define as one atomic mass unit (amu) or one Dalton.
• Each electron has a negative charge (-1) equal to the positive charge of a proton (+1).
• Neutrons are uncharged particles found within the nucleus.

Key Terms

• atom: The smallest possible amount of matter which still retains its identity as a chemical element, consisting of a nucleus surrounded by electrons.
• proton: Positively charged subatomic particle forming part of the nucleus of an atom and determining the atomic number of an element. It weighs 1 amu.
• neutron: A subatomic particle forming part of the nucleus of an atom. It has no charge. It is equal in mass to a proton or it weighs 1 amu.

C) The atomic number of an atom is equivalent to the number of protons in the nucleus. A) The mass number of an atom is equal to the number of protons plus the number of nucleons in the nucleus. The collective name for these is nucleons. B) A specific atom of molybdenum has an atomic number of 42 and a mass number of 96. The atomic number is the number of protons in an atom, and isotopes have the same atomic number but differ in the number of neutrons. Fundamental properties of atoms including atomic number and atomic.

An atom is the smallest unit of matter that retains all of the chemical properties of an element. Atoms combine to form molecules, which then interact to form solids, gases, or liquids. For example, water is composed of hydrogen and oxygen atoms that have combined to form water molecules. Many biological processes are devoted to breaking down molecules into their component atoms so they can be reassembled into a more useful molecule.

Atomic Particles

Atoms consist of three basic particles: protons, electrons, and neutrons. The nucleus (center) of the atom contains the protons (positively charged) and the neutrons (no charge). The outermost regions of the atom are called electron shells and contain the electrons (negatively charged). Atoms have different properties based on the arrangement and number of their basic particles.

The hydrogen atom (H) contains only one proton, one electron, and no neutrons. This can be determined using the atomic number and the mass number of the element (see the concept on atomic numbers and mass numbers).

Structure of an atom: Elements, such as helium, depicted here, are made up of atoms. Atoms are made up of protons and neutrons located within the nucleus, with electrons in orbitals surrounding the nucleus.

Atomic Mass

Protons and neutrons have approximately the same mass, about 1.67 × 10^-24 grams. Scientists define this amount of mass as one atomic mass unit (amu) or one Dalton. Although similar in mass, protons are positively charged, while neutrons have no charge. Therefore, the number of neutrons in an atom contributes significantly to its mass, but not to its charge.

Electrons are much smaller in mass than protons, weighing only 9.11 × 10^-28 grams, or about 1/1800 of an atomic mass unit. Therefore, they do not contribute much to an element’s overall atomic mass. When considering atomic mass, it is customary to ignore the mass of any electrons and calculate the atom’s mass based on the number of protons and neutrons alone.

Electrons contribute greatly to the atom’s charge, as each electron has a negative charge equal to the positive charge of a proton. Scientists define these charges as “+1” and “-1. ” In an uncharged, neutral atom, the number of electrons orbiting the nucleus is equal to the number of protons inside the nucleus. In these atoms, the positive and negative charges cancel each other out, leading to an atom with no net charge.

Protons, neutrons, and electrons: Both protons and neutrons have a mass of 1 amu and are found in the nucleus. However, protons have a charge of +1, and neutrons are uncharged. Electrons have a mass of approximately 0 amu, orbit the nucleus, and have a charge of -1.

Exploring Electron Properties: Compare the behavior of electrons to that of other charged particles to discover properties of electrons such as charge and mass.

Volume of Atoms

Accounting for the sizes of protons, neutrons, and electrons, most of the volume of an atom—greater than 99 percent—is, in fact, empty space. Despite all this empty space, solid objects do not just pass through one another. The electrons that surround all atoms are negatively charged and cause atoms to repel one another, preventing atoms from occupying the same space. These intermolecular forces prevent you from falling through an object like your chair.

Interactive: Build an Atom: Build an atom out of protons, neutrons, and electrons, and see how the element, charge, and mass change. Then play a game to test your ideas!

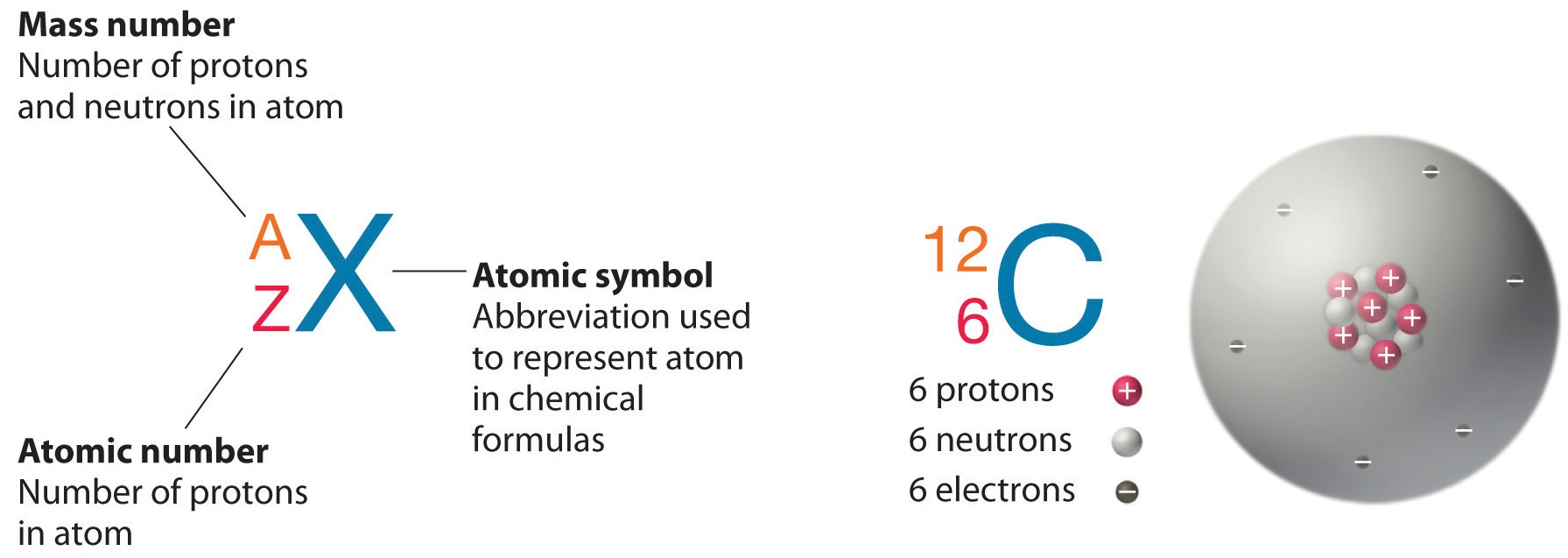
Atomic Number and Mass Number

The atomic number is the number of protons in an element, while the mass number is the number of protons plus the number of neutrons.

Learning Objectives

Determine the relationship between the mass number of an atom, its atomic number, its atomic mass, and its number of subatomic particles

Key Takeaways

Key Points

• Neutral atoms of each element contain an equal number of protons and electrons.
• The number of protons determines an element’s atomic number and is used to distinguish one element from another.
• The number of neutrons is variable, resulting in isotopes, which are different forms of the same atom that vary only in the number of neutrons they possess.
• Together, the number of protons and the number of neutrons determine an element’s mass number.
• Since an element’s isotopes have slightly different mass numbers, the atomic mass is calculated by obtaining the mean of the mass numbers for its isotopes.

Key Terms

• mass number: The sum of the number of protons and the number of neutrons in an atom.
• atomic number: The number of protons in an atom.
• atomic mass: The average mass of an atom, taking into account all its naturally occurring isotopes.

Atomic Number

Atomic Number Of An Atom Is The

Neutral atoms of an element contain an equal number of protons and electrons. The number of protons determines an element’s atomic number (Z) and distinguishes one element from another. For example, carbon’s atomic number (Z) is 6 because it has 6 protons. The number of neutrons can vary to produce isotopes, which are atoms of the same element that have different numbers of neutrons. The number of electrons can also be different in atoms of the same element, thus producing ions (charged atoms). For instance, iron, Fe, can exist in its neutral state, or in the +2 and +3 ionic states.

Mass Number

An element’s mass number (A) is the sum of the number of protons and the number of neutrons. The small contribution of mass from electrons is disregarded in calculating the mass number. This approximation of mass can be used to easily calculate how many neutrons an element has by simply subtracting the number of protons from the mass number. Protons and neutrons both weigh about one atomic mass unit or amu. Isotopes of the same element will have the same atomic number but different mass numbers.

Atomic number, chemical symbol, and mass number: Carbon has an atomic number of six, and two stable isotopes with mass numbers of twelve and thirteen, respectively. Its average atomic mass is 12.11.

Scientists determine the atomic mass by calculating the mean of the mass numbers for its naturally-occurring isotopes. Often, the resulting number contains a decimal. For example, the atomic mass of chlorine (Cl) is 35.45 amu because chlorine is composed of several isotopes, some (the majority) with an atomic mass of 35 amu (17 protons and 18 neutrons) and some with an atomic mass of 37 amu (17 protons and 20 neutrons).

Given an atomic number (Z) and mass number (A), you can find the number of protons, neutrons, and electrons in a neutral atom. For example, a lithium atom (Z=3, A=7 amu) contains three protons (found from Z), three electrons (as the number of protons is equal to the number of electrons in an atom), and four neutrons (7 – 3 = 4).

Isotopes

Isotopes are various forms of an element that have the same number of protons, but a different number of neutrons.

Learning Objectives

Discuss the properties of isotopes and their use in radiometric dating

Key Takeaways

Key Points

• Isotopes are atoms of the same element that contain an identical number of protons, but a different number of neutrons.
• Despite having different numbers of neutrons, isotopes of the same element have very similar physical properties.
• Some isotopes are unstable and will undergo radioactive decay to become other elements.
• The predictable half-life of different decaying isotopes allows scientists to date material based on its isotopic composition, such as with Carbon-14 dating.

Key Terms

• isotope: Any of two or more forms of an element where the atoms have the same number of protons, but a different number of neutrons within their nuclei.
• half-life: The time it takes for half of the original concentration of an isotope to decay back to its more stable form.
• radioactive isotopes: an atom with an unstable nucleus, characterized by excess energy available that undergoes radioactive decay and creates most commonly gamma rays, alpha or beta particles.
• radiocarbon dating: Determining the age of an object by comparing the ratio of the 14C concentration found in it to the amount of 14C in the atmosphere.

What is an Isotope?

Isotopes are various forms of an element that have the same number of protons but a different number of neutrons. Some elements, such as carbon, potassium, and uranium, have multiple naturally-occurring isotopes. Isotopes are defined first by their element and then by the sum of the protons and neutrons present.

• Carbon-12 (or ¹²C) contains six protons, six neutrons, and six electrons; therefore, it has a mass number of 12 amu (six protons and six neutrons).
• Carbon-14 (or ¹⁴C) contains six protons, eight neutrons, and six electrons; its atomic mass is 14 amu (six protons and eight neutrons).

While the mass of individual isotopes is different, their physical and chemical properties remain mostly unchanged.

Isotopes do differ in their stability. Carbon-12 (¹²C) is the most abundant of the carbon isotopes, accounting for 98.89% of carbon on Earth. Carbon-14 (¹⁴C) is unstable and only occurs in trace amounts. Unstable isotopes most commonly emit alpha particles (He²⁺) and electrons. Neutrons, protons, and positrons can also be emitted and electrons can be captured to attain a more stable atomic configuration (lower level of potential energy ) through a process called radioactive decay. The new atoms created may be in a high energy state and emit gamma rays which lowers the energy but alone does not change the atom into another isotope. These atoms are called radioactive isotopes or radioisotopes.

Radiocarbon Dating

Carbon is normally present in the atmosphere in the form of gaseous compounds like carbon dioxide and methane. Carbon-14 (¹⁴C) is a naturally-occurring radioisotope that is created from atmospheric ¹⁴N (nitrogen) by the addition of a neutron and the loss of a proton, which is caused by cosmic rays. This is a continuous process so more ¹⁴C is always being created in the atmosphere. Once produced, the ¹⁴C often combines with the oxygen in the atmosphere to form carbon dioxide. Carbon dioxide produced in this way diffuses in the atmosphere, is dissolved in the ocean, and is incorporated by plants via photosynthesis. Animals eat the plants and, ultimately, the radiocarbon is distributed throughout the biosphere.

In living organisms, the relative amount of ¹⁴C in their body is approximately equal to the concentration of ¹⁴C in the atmosphere. When an organism dies, it is no longer ingesting ¹⁴C, so the ratio between ¹⁴C and ¹²C will decline as ¹⁴C gradually decays back to ¹⁴N. This slow process, which is called beta decay, releases energy through the emission of electrons from the nucleus or positrons.

After approximately 5,730 years, half of the starting concentration of ¹⁴C will have been converted back to ¹⁴N. This is referred to as its half-life, or the time it takes for half of the original concentration of an isotope to decay back to its more stable form. Because the half-life of ¹⁴C is long, it is used to date formerly-living objects such as old bones or wood. Comparing the ratio of the ¹⁴C concentration found in an object to the amount of ¹⁴C in the atmosphere, the amount of the isotope that has not yet decayed can be determined. On the basis of this amount, the age of the material can be accurately calculated, as long as the material is believed to be less than 50,000 years old. This technique is called radiocarbon dating, or carbon dating for short.

Application of carbon dating: The age of carbon-containing remains less than 50,000 years old, such as this pygmy mammoth, can be determined using carbon dating.

Other elements have isotopes with different half lives. For example, ⁴⁰K (potassium-40) has a half-life of 1.25 billion years, and ²³⁵U (uranium-235) has a half-life of about 700 million years. Scientists often use these other radioactive elements to date objects that are older than 50,000 years (the limit of carbon dating). Through the use of radiometric dating, scientists can study the age of fossils or other remains of extinct organisms.

A total of four quantum numbers are used to describe completely the movement and trajectories of each electron within an atom. The combination of all quantum numbers of all electrons in an atom is described by a wave function that complies with the Schrödinger equation. Each electron in an atom has a unique set of quantum numbers; according to the Pauli Exclusion Principle, no two electrons can share the same combination of four quantum numbers. Quantum numbers are important because they can be used to determine the electron configuration of an atom and the probable location of the atom's electrons. Quantum numbers are also used to understand other characteristics of atoms, such as ionization energy and the atomic radius.

In atoms, there are a total of four quantum numbers: the principal quantum number (n), the orbital angular momentum quantum number (l), the magnetic quantum number (m_l), and the electron spin quantum number (m_s). The principal quantum number, (n), describes the energy of an electron and the most probable distance of the electron from the nucleus. In other words, it refers to the size of the orbital and the energy level an electron is placed in. The number of subshells, or (l), describes the shape of the orbital. It can also be used to determine the number of angular nodes. The magnetic quantum number, m_l, describes the energy levels in a subshell, and m_s refers to the spin on the electron, which can either be up or down.

The Principal Quantum Number ((n))

The principal quantum number, (n), designates the principal electron shell. Because n describes the most probable distance of the electrons from the nucleus, the larger the number n is, the farther the electron is from the nucleus, the larger the size of the orbital, and the larger the atom is. n can be any positive integer starting at 1, as (n=1) designates the first principal shell (the innermost shell). The first principal shell is also called the ground state, or lowest energy state. This explains why (n) can not be 0 or any negative integer, because there exists no atoms with zero or a negative amount of energy levels/principal shells. When an electron is in an excited state or it gains energy, it may jump to the second principle shell, where (n=2). This is called absorption because the electron is 'absorbing' photons, or energy. Known as emission, electrons can also 'emit' energy as they jump to lower principle shells, where n decreases by whole numbers. As the energy of the electron increases, so does the principal quantum number, e.g., n = 3 indicates the third principal shell, n = 4 indicates the fourth principal shell, and so on.

[n=1,2,3,4…]

Example (PageIndex{1})

If n = 7, what is the principal electron shell?

Example (PageIndex{2})

If an electron jumped from energy level n = 5 to energy level n = 3, did absorption or emission of a photon occur?

Answer

Atomic Number Of An Atom Represents

Emission, because energy is lost by release of a photon.

The Orbital Angular Momentum Quantum Number ((l))

The orbital angular momentum quantum number (l) determines the shape of an orbital, and therefore the angular distribution. The number of angular nodes is equal to the value of the angular momentum quantum number (l). (For more information about angular nodes, see Electronic Orbitals.) Each value of (l) indicates a specific s, p, d, f subshell (each unique in shape.) The value of (l) is dependent on the principal quantum number (n). Unlike (n), the value of (l) can be zero. It can also be a positive integer, but it cannot be larger than one less than the principal quantum number ((n-1)):

[l=0, 1, 2, 3, 4…, (n-1)]

Example (PageIndex{3})

If (n = 7), what are the possible values of (l)?

Answer

Since (l) can be zero or a positive integer less than ((n-1)), it can have a value of 0, 1, 2, 3, 4, 5 or 6.

Example (PageIndex{4})

If (l = 4), how many angular nodes does the atom have?

Answer

The number of angular nodes is equal to the value of l, so the number of nodes is also 4.

The Magnetic Quantum Number ((m_l))

The magnetic quantum number (m_l) determines the number of orbitals and their orientation within a subshell. Consequently, its value depends on the orbital angular momentum quantum number (l). Given a certain (l), (m_l) is an interval ranging from (–l) to (+l), so it can be zero, a negative integer, or a positive integer.

[m_l= -l, (-l +1),( -l +2),…, -2, -1, 0, 1, 2, … (l – 1), (l – 2), +l]

Example (PageIndex{5})

Example: If (n=3), and (l=2), then what are the possible values of (m_l)?

Answer

Since (m_l) must range from (–l) to (+l), then (m_l) can be: -2, -1, 0, 1, or 2.

The Electron Spin Quantum Number ((m_s))

Unlike (n), (l), and (m_l), the electron spin quantum number (m_s) does not depend on another quantum number. It designates the direction of the electron spin and may have a spin of +1/2, represented by↑, or –1/2, represented by ↓. This means that when (m_s) is positive the electron has an upward spin, which can be referred to as 'spin up.' When it is negative, the electron has a downward spin, so it is 'spin down.' The significance of the electron spin quantum number is its determination of an atom's ability to generate a magnetic field or not. (Electron Spin.)

[m_s= pm dfrac{1}{2}]

Example (PageIndex{5})

List the possible combinations of all four quantum numbers when (n=2), (l=1), and (m_l=0).

Answer

The fourth quantum number is independent of the first three, allowing the first three quantum numbers of two electrons to be the same. Since the spin can be +1/2 or =1/2, there are two combinations:

• (n=2), (l=1), (m_l =0), (m_s=+1/2)
• (n=2), (l=1), (m_l=0), (m_s=-1/2)

Example (PageIndex{6})

Can an electron with (m_s=1/2) have a downward spin?

Answer

No, if the value of (m_s) is positive, the electron is 'spin up.'

A Closer Look at Shells, Subshells, and Orbitals

Principal Shells

The value of the principal quantum number n is the level of the principal electronic shell (principal level). All orbitals that have the same n value are in the same principal level. For example, all orbitals on the second principal level have a principal quantum number of n=2. When the value of n is higher, the number of principal electronic shells is greater. This causes a greater distance between the farthest electron and the nucleus. As a result, the size of the atom and its atomic radius increases.

Because the atomic radius increases, the electrons are farther from the nucleus. Thus it is easier for the atom to expel an electron because the nucleus does not have as strong a pull on it, and the ionization energy decreases.

Example (PageIndex{7})

Which orbital has a higher ionization energy, one with (n=3) or (n=2)?

Answer

The orbital with n=2, because the closer the electron is to the nucleus or the smaller the atomic radius, the more energy it takes to expel an electron.

Subshells

The number of values of the orbital angular number l can also be used to identify the number of subshells in a principal electron shell:

• When n = 1, l= 0 (l takes on one value and thus there can only be one subshell)
• When n = 2, l= 0, 1 (l takes on two values and thus there are two possible subshells)
• When n = 3, l= 0, 1, 2 (l takes on three values and thus there are three possible subshells)

After looking at the examples above, we see that the value of n is equal to the number of subshells in a principal electronic shell:

• Principal shell with n = 1 has one subshell
• Principal shell with n = 2 has two subshells
• Principal shell with n = 3 has three subshells

To identify what type of possible subshells n has, these subshells have been assigned letter names. The value of l determines the name of the subshell:

Name of Subshell	Value of (l)
s subshell	0
p subshell	1
d subshell	2
f subshell	3

Therefore:

• Principal shell with n = 1 has one s subshell (l = 0)
• Principal shell with n = 2 has one s subshell and one p subshell (l = 0, 1)
• Principal shell with n = 3 has one s subshell, one p subshell, and one d subshell (l = 0, 1, 2)

We can designate a principal quantum number, n, and a certain subshell by combining the value of n and the name of the subshell (which can be found using l). For example, 3p refers to the third principal quantum number (n=3) and the p subshell (l=1).

Example (PageIndex{8})

What is the name of the orbital with quantum numbers n=4 and l=1?

Answer

Knowing that the principal quantum number n is 4 and using the table above, we can conclude that it is 4p.

Example (PageIndex{9})

What is the name of the oribital(s) with quantum number n=3?

Atomic Number Of An Atom Or Element Is The Number Of

Answer

3s, 3p, and 3d. Because n=3, the possible values of l = 0, 1, 2, which indicates the shapes of each subshell.

Orbitals

The number of orbitals in a subshell is equivalent to the number of values the magnetic quantum number ml takes on. A helpful equation to determine the number of orbitals in a subshell is 2l +1. This equation will not give you the value of ml, but the number of possible values that ml can take on in a particular orbital. For example, if l=1 and ml can have values -1, 0, or +1, the value of 2l+1 will be three and there will be three different orbitals. The names of the orbitals are named after the subshells they are found in:

s orbitals	p orbitals	d orbitals	f orbitals
l	0	1	2	3
ml	0	-1, 0, +1	-2, -1, 0, +1, +2	-3, -2, -1, 0, +1, +2, +3
Number of orbitals in designated subshell	1	3	5	7

In the figure below, we see examples of two orbitals: the p orbital (blue) and the s orbital (red). The red s orbital is a 1s orbital. To picture a 2s orbital, imagine a layer similar to a cross section of a jawbreaker around the circle. The layers are depicting the atoms angular nodes. To picture a 3s orbital, imagine another layer around the circle, and so on and so on. The p orbital is similar to the shape of a dumbbell, with its orientation within a subshell depending on m_l. The shape and orientation of an orbital depends on l and m_l.

To visualize and organize the first three quantum numbers, we can think of them as constituents of a house. In the following image, the roof represents the principal quantum number n, each level represents a subshell l, and each room represents the different orbitals ml in each subshell. The s orbital, because the value of ml can only be 0, can only exist in one plane. The p orbital, however, has three possible values of ml and so it has three possible orientations of the orbitals, shown by Px, Py, and Pz. The pattern continues, with the d orbital containing 5 possible orbital orientations, and f has 7:

Another helpful visual in looking at the possible orbitals and subshells with a set of quantum numbers would be the electron orbital diagram. (For more electron orbital diagrams, see Electron Configurations.) The characteristics of each quantum number are depicted in different areas of this diagram.

Restrictions

• Pauli Exclusion Principle: In 1926, Wolfgang Pauli discovered that a set of quantum numbers is specific to a certain electron. That is, no two electrons can have the same values for n, l, ml, and ms. Although the first three quantum numbers identify a specific orbital and may have the same values, the fourth is significant and must have opposite spins.
• Hund's Rule: Orbitals may have identical energy levels when they are of the same principal shell. These orbitals are called degenerate, or 'equal energy.' According to Hund's Rule, electrons fill orbitals one at a time. This means that when drawing electron configurations using the model with the arrows, you must fill each shell with one electron each before starting to pair them up. Remember that the charge of an electron is negative and electrons repel each other. Electrons will try to create distance between it and other electrons by staying unpaired. This further explains why the spins of electrons in an orbital are opposite (i.e. +1/2 and -1/2).
• Heisenberg Uncertainty Principle: According to the Heisenberg Uncertainty Principle, we cannot precisely measure the momentum and position of an electron at the same time. As the momentum of the electron is more and more certain, the position of the electron becomes less certain, and vice versa. This helps explain integral quantum numbers and why n=2.5 cannot exist as a principal quantum number. There must be an integral number of wavelengths (n) in order for an electron to maintain a standing wave. If there were to be partial waves, the whole and partial waves would cancel each other out and the particle would not move. If the particle was at rest, then its position and momentum would be certain. Because this is not so, n must have an integral value. It is not that the principal quantum number can only be measured in integral numbers, it is because the crest of one wave will overlap with the trough of another, and the wave will cancel out.

References

1. Chang, Raymond. Physical Chemistry for the Biosciences. 2005, University Science Books. pp 427-428.
2. Gillespie, Ronald. Demystifying Introductory Chemistry. The Forum: A Contribution from the Task Force on General Chemistry. 1996: 73;617-622.
3. Petrucci, Ralph. General Chemistry: Principles and Modern Applications, Tenth Edition.

What Does The Atomic Number Tell Us

Problems

1. Suppose that all you know about a certain electron is that its principal quantum number is 3. What are the possible values for the other four quantum numbers?
2. Is it possible to have an electron with these quantum numbers: (n=2), (l=1), (m_l=3), (m_s=1/2)? Why or why not?
3. Is it possible to have two electrons with the same (n), (l), and (m_l)?
4. How many subshells are in principal quantum level (n=3)?
5. What type of orbital is designated by quantum numbers (n=4), (l=3), and (m_l =0)?

What Does Atomic Number Mean

Solutions

1. • When (n=3), ( l=0), (m_l = 0), and (m_s=+1/2 text{ or } -1/2)
   • (l=1), (m_l = -1, 0, or +1), and (m_s=+1/2 text{ or } -1/2)
   • (l=2), (m_l = -2, -1, 0, 1, text{ or }+2), and (m_s=+1/2 text{ or } -1/2)
2. No, it is not possible. (m_l=3) is not in the range of (-l) to (+l). The value should be be either -1, 0, or +1.
3. Yes, it is possible to have two electrons with the same (n), (l), and (m_l). The spin of one electron must be +1/2 while the spin of the other electron must be -1/2.
4. There are three subshells in principal quantum level (n=3).
5. Since (l=3) refers to the f subshell, the type of orbital represented is 4f (combination of the principal quantum number n and the name of the subshell).

Contributors and Attributions

Atomic Number Of An Atom

• Anastasiya Kamenko, Tamara Enriquez (UCD), Mandy Lam (UCD)

• Dr. Craig Fisher (Japan Fine Ceramics Center)